|
|
 How to Give Villains Bad Odds with "Made Hands" How to Give Villains Bad Odds with "Made Hands"
Assume a no-limit hold'em game with blinds at $1/2, 7 players with $100 effective stacks and no rake. Preflop it's folded to you in MP and you raise to $7 with T  9 9  and only the big blind calls. The pot is $15. The flop comes J and only the big blind calls. The pot is $15. The flop comes J  7 7  8 8  . The big blind checks, you bet $12.50, and the big blind calls. The pot is $40. The turn makes the board J . The big blind checks, you bet $12.50, and the big blind calls. The pot is $40. The turn makes the board J  7 7  8 8  2 2 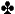 . The big blind checks. How much should we bet? . The big blind checks. How much should we bet?
First we need to know how much money we have left behind. We bet $7 preflop with an additional $12.50 put in on the flop, so that leaves us with $80.50 behind with a pot of $40. Here are three questions and answers that we should be able to answer in any situation where we have a "made hand" and are likely playing against a "drawing hand".
Q1. What is villain's most likely draw?
A1. A nine-out flush draw. A set has another strong draw here, but it's doubtful that villain would check/call with a set on this coordinated of a flop.
Q2. If a scare card comes off on the river (in this case a third spade) can we get away from our hand?
A2. Our hand is probably too strong to get away from. The answer to this question dictates how we should play the rest of the hand. In this post I'm going to focus on when we decide we can't get away from the hand when a scare card comes because it's the simplest case and everything else isn't much more complicated.
Q3. What are our opponent's implied odds assuming we're stacking off on the river even when a scare card comes?
A3. Our Stack Before We Bet + The Pot Before We Bet : Our Bet Size. If we bet $20 in the above example, then our opponent's implied odds on our stack are $80.50 + $40 : $20 or $120.50 : $20, or about 6:1.
Here is the idea: Since we have decided that we can't get away from this hand if the scare card comes, we want to adjust our betting so that we're always going to call on the river AND we're always going to be profitable.
(Note: This isn't always going to be practical if there is a lot of money behind. In that case, you should change your assessment of always stacking off no matter what river card comes.)
Quick example: In the above hand we decide that villain has at most 9 outs. We also have $80.50 behind with a pot of $40. If we bet $32, then villain is calling $32 to win $120.50 (our stack plus the current pot). He's getting 120.50:32 or 3.8:1 implied odds. Villain needs implied odds of 36:9 or 4:1 to break even on a call assuming he has 9 outs (a flush draw) and we always stack off on the river when he hits his flush (but never when he does not). His implied odds aren't good enough here so we profit when he calls the $32 bet -- regardless of what happens after that.
Now figure out more complicated examples and post them here for everyone to discuss. Gogogogo.
|
9
and only the big blind calls. The pot is $15. The flop comes J
7
8
. The big blind checks, you bet $12.50, and the big blind calls. The pot is $40. The turn makes the board J
7
8
2
. The big blind checks. How much should we bet?




 Reply With Quote
Reply With Quote






