|
|
 Folding equity example (high math content) Folding equity example (high math content)
Hypothetical hand:
100NL 6-max table, effective stacks are $100
UTG limps, 2 folds and Hero raises to $3 on the button with 8 7 7
SB calls and UTG calls
Flop: 6 K K J J (Pot is $10) (Pot is $10)
SB checks, UTG bets $8, Hero raises to $20 (feeling frisky), SB folds and UTG calls
Turn: 5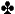 (Pot is $50) (Pot is $50)
UTG bets $25, Hero raises to $77 and is all-in.
We want to calculate how much folding equity we need to make the turn push profitable.
When UTG folds we win $75, when UTG calls and we win the showdown we win $127 but when UTG calls and we lose the showdown we lose $77.
(Notice we are just using the net effect the push has on our stack at that point)
So:
EV(folds) = $75
EV(win) = $127
EV(lose) = -$77
P(folds) is the probability that UTG will fold (between 0 and 1, 0 corresponds to 0% and 1 corresponds to 100%)
P(calls) is the probability that UTG will call and since his only options are call or fold, P(folds)+P(calls) = 1. If he calls 40% (0.4) of the time it means he must fold 60%(0.6) of the time.
Overall our expected value is:
EV = P(folds)*EV(folds) + P(calls)*EV(calls)
and P(calls) = 1-P(folds) and EV(folds) = $75 so the equation becomes:
EV = P(folds)*75 + (1-P(folds))*EV(calls)
Our folding equity is the left part of the equation (P(folds)*75) and we want to solve for what value of P(folds) our overall expected value is positive. In other words how often does our opponent need to fold for this to be a good push.Normally when we need to calculate this it is because we expect to take the worse of it when the opponent calls and therefore the
right hand side of the equation (1-P(folds))*EV(calls) is expected to be negative so our folding equity needs to be big enough to make our overall expected value positive.
We still have two unknowns and therefore we cannot solve the equation yet so we need to calculate what our expected value is when our opponent calls (EV(calls)).
To do this we need to assign a hand range to our opponent and see how often our hand wins against that range. Lets assume our opponent will call us with one of the following hands: AA,KK,AK,KQ,KJ,JJ,66
From PokerStove:
Board: 6s Kd Jd 5c
Dead:
equity (%) win (%) tie (%)
Hand 1: 32.8125 % 32.81% 00.00% { 8d7d }
Hand 2: 67.1875 % 67.19% 00.00% { KK+, JJ, 66, AKs, KJs+, AKo, KJo+ }
So our probability to win the hand when called is 32.8125% or 0.328125
So
EV(calls) = P(win)*EV(win) + P(lose)*EV(lose)
= 0.328125*(127) + 0.671875*(-77)
= -10.0625
Substituting this back into our original equation we get:
EV = P(folds)*75 + (1-P(folds))*(-10.0625)
= P(folds)*75 -10.0625 + 10.0625*P(folds)
= 85.0625*P(folds) - 10.0625
The breakeven point is where our EV is 0 so
0 = 85.0625*P(folds) - 10.0625
10.0625 = 85.0625*P(folds)
P(folds) = 0.1183
So if we can get our opponent to fold 12% of the time or more the push is profitable even though our flop raise probably wasn't. This is due to the dead money in the pot (created by the flop raise) and that we still have a lot of outs.
Please point out any mistakes and I will correct them.
|
7

K
J
(Pot is $10)
(Pot is $50)




 Reply With Quote
Reply With Quote

