|
|
 Probability question (math nerds welcome) Probability question (math nerds welcome)
So I've been trying to study variance as it applies to poker, and I'm a little confused on something. I'll give an example.
Suppose its the river and you're calling a bet of one unit into a pot of one unit, with exactly a 1/3 chance of winning. You call and the EV is 0 units, which is the arithmetic mean. There are two outcomes, one in which you lose one unit 2/3 of the time and one in which you gain two units 1/3 of the time.
My cursory knowledge of probability theory says that the variance is as follows:
Variance = Sum of (Probability of outcome)(distance from mean ^2) for all outcomes
V = (1/3)(2^2) + (2/3)(1^2)
V = 2 units^2 / trials^2
Standard Deviation = sqrt(V)
σ = 1.414 units / trial
OK, so now I want to know what 95% of my range of values near the mean will be for 100 trials. I'm pretty sure this is what a confidence interval is, but it's possible that I may be misunderstanding the term. Anyway to calculate the 95% confidence interval after 100 trials:
670px-Calculate-Confidence-Interval-Step-5-Version-4.jpg
According to a statistics book, Z for 95% is 1.92. Since V is additive for trials, V for 100 trials = 200, so σ for 100 trials is sqrt(200) = 14.14, thus the standard error is as follows:
Standard Error = 1.92 x 14.14/sqrt(100) = 2.715, and my 95% confidence range is (-2.715 units, +2.715 units).
To me, this seems unbelievably small, so I'm not sure this range is describing what I want to know. Suppose I take a brute force approach.
If I call this bet 100 times, there are exactly 101 different outcomes. I could win 100 times, or win 99 times, or win 98 times, and so on until winning zero times. The probabilities of these outcomes are very easy to establish, for example:
P(win 100) = (1/3)^100, EV(win 100) = 200 units
P(win 99) = 100*(2/3)*(1/3)^99, EV(win 99) = 197 units
etc
etc
P(win 1) = 100*(1/3)*(2/3)^99, EV(win 1) = -97 units
P(win 0) = (2/3)^100, EV(win 0) = -100 units
Intuitively it seems clear that the highest probability outcome will be winning 33 times, and that probability of the outcomes will descend smoothly away from that. So if I did all this arithmetic, and added the highest probability outcomes until I reached 95%, would all of those outcomes fall within the (-2.715 units, +2.715 units) range?
Apologies if I wasn't very clear in my explanation, let me know if you need clarification on something.
Thanks
|




 Reply With Quote
Reply With Quote

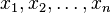 , usually denoted by
, usually denoted by 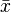 , is the sum of the sampled values divided by the number of items in the sample:
, is the sum of the sampled values divided by the number of items in the sample: