GTO and Frequencies
Been thinking about/ reading about Game Theory more lately and just frequencies in general.
One spot I think I lack is really using the appropriate frequencies in spots. I tend to go to extremes too often, either not triple barrel bluffing or doing it too much. I've always find it hard to figure out a way to really control frequencies.
Known:
If we bet on the river:
50% of the pot - Villain needs to call and win 25% of the time (ie: We can bluff 25% of the time)
60% of pot - We can bluff 27% of the time
70% of pot -We can bluff 29.6% of the time
80% of pot - We can bluff 30.7% of the time
90% of pot - We can bluff 32.1% of the time
100% of the pot - We can bluff 33% of the time
But how can we control this in practice, and be bluffing with the appropriate number of combos relative to value hands?
After a bit of math I've come up with:
Bluff combos = (%wecanbluff * num_value_hands)/(1-%wecanbluff)
So if we can bluff 27% of the time, this simplifies to:
Bluff combos = 0.37*numvaluehands
If we can bluff 30.7% of the time, this simplifies to:
Bluff combos = 0.44*numvaluehands
So really, the amount that will satisfy most of our betting range on the river (between 0.6-0.8 of the pot) will be:
Bluff combos = 0.4*numvaluehands
**DISCLAIMER** - I don't think content below here in this post is correct, tried fixing it in the subsequent post ***
How to put into practice?
Suppose we're on the turn with
The board is


I'm going to estimate we have 15 outs (so 15 cards on the river we'll be betting for value - 9 hearts, 3 non heart K, 3 non heart Q)
Bluff combos = 0.4*15
Bluff combos = 6 combos
Knowing we can put this into practice, the best way to do this is to decide on the turn which 6 combos you will bluff with. This will work out to picking two cards in the deck to bluff on (3 non-heart cards per selection).
In this case the cards with the most fold equity are likely any Ace and any Jack (6 non heart aces and jacks). If we decide on the turn that we will always bluff any ace and any jack, but also ONLY bluff any ace and any jack, we will be bluffing with 6 combos compared to 15 value combos (28.5% bluffs).
If we bet a little less than 70% on the river, then we are playing GTO vs his calling range. We are indifferent to villain calling or folding to our bet. This is on top of the times he incorrectly folds to our bets on an A or J river.
Common draws:
OESD = 8 value outs, need 3 bluffs
FD = 9 value outs, need about 3 bluffs (3.6 really) - so pick one card in the deck and bet all of those rivers when that card falls
FD+1 over = 12 value outs, need 4.8 bluffs
FD+gutter = 13 value outs, need 5 bluffs
FD+2 overs = 15 value outs, bet 6 combos for bluffs
I'll try to put this into practice. The key here is that you're pre-selecting your bluff cards on the turn and sticking to it. If you just randomly decide on the river, then its tough to really control frequencies.
(Important note: Playing GTO assumes that your opponent is also playing close to GTO. If villain has exploitable tendencies (ie: folds way too much or way too little), this would not be the best gameplan)




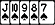




 Reply With Quote
Reply With Quote