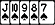|
|
1) With a pot sized raise, villain needs us to fold 64.3% of the time to make a profit (not counting his equity with KQ if we continue)
My cbet range:
Check 77-99,AKs,QTs,JTs,T9s,T8s,78s,AKo,QTo,JTo
Bet TT+,66-22,AQs-A6s,K7s+,QJs,Q9s-Q8s,J9s,97s+,86s,76s,AQo-ATo,KTo+,QJo
Board: Ts6c5d
Villain has KQ
Combos:
TT(3),JJ(6),KK(3),QQ(3),55-66(6),22-44(18),A6s(3),A9s-a7s(12),ATs(3),AQs(3),AJs(4),K7s-K9s(9),KTs(2),KQs(3),KJs(3),QJs(3),Q9s-Q8s(6),J9s(4),97s+(8),86s(3),76s(3),AQo(9),AJo(12) ,ATo(9),KTo(7),KQo(6),KJo(9),QJo(9)
Total combos = 169
Fold to a pot sized raise:
Now comes the tough question of whether we fold overpairs and top pair top kicker facing his pot-sized raise. Let's see. In part 1, I had villain raising the flop with TPTK or better: AT,TT,55,66 (overpairs are not in his range as I assumed he would have reraised these preflop). With top pair, against this range, I have 24% equity or less (depending on the kicker). The pot odds are 33%, so I can't continue. With overpairs, I have 41% or better, so I would continue with these. So I fold everything except overpairs and sets. Overpairs and sets are 21 combos out of 169, so I would fold 87.8% of my cbet range to his pot sized raise.
87.8% >> 64.3%, so indeed, I am vulnerable to him playing back at me.
2) If he calls the flop, from exercise 1, I have him on JTs,T9s,98s,87s,JTo,T9o, and subtracting my turn betting range (TT+,66-55,AJs-ATs,KJs-KTs,QJs,J9s,AJo-ATo,KJo-KTo) from my flop cbetting range, I would check with:
22-44(18),A6s(3),A9s-a7s(12),AQs(3),K7s-K9s(9),KQs(3),Q9s-Q8s(6),97s+(8),86s(3),76s(3),AQo(9),KQo(6)
That is 83 combos, or 49.1% of my flop cbetting range.
He makes a 2/3rd pot bet, laying 28.6% pot odds, and I will assume he does that with his entire range facing the weak turn check. I would call this based on implied odds with:
As9s(1),As8s(1),As7s(1),As6s(1),AsQs(1),Ks9s(1),Ks 8s(1),Ks7s(1),KQs(3),Qs9s(1),Qs8s(1),9s7s(1),8s6s( 1),7s6s(1),KQo(6)
That is 22 combos, but I will discount to 20 combos for the times he has the Ks or Qs.
So I fold to his turn bet with 63 out of 83 combos or 75.9% of my checking range.
So I check/fold the turn 0.491*0.759 = 37.3% of the time after cbetting the flop.
Since 37.3% << 58%, his float is not immediately profitable, but let's not forget that he still has showdown equity in the hand with his KQ. Also, in this case, the float is not immediately profitable because we got a turn card that is favoring our range. Many times, this will not be the case. So I would suspect that the float is still a good play most of the time.
3) I am vulnerable because I defined my cbet range against a guy who I think plays fit or fold but in fact he has realized what I am doing and he's playing back at me by raising with overcards. Basically, I am overestimating my fold equity. How do I adjust to him playing back? Well if he is the same nit who is only playing back with hands that have some decent equity, like his KQ, then to defend against a flop raise, I should cbet much less of my air (check the flop with the worse part of my air). To defend against a float, I can also cbet less of my air, but another thing I can do is second barrel more.
If the nit has become a maniac who systematically raises or floats my cbets, then I will start re-including my fair hands like second pairs into my cbetting range, and dumping the air from it. Then I can call or shove over his raises or second barrel his floats with hands that have decent equity.
|
Originally Posted by spoonitnow



 6
6  5
5  .
. 
 Reply With Quote
Reply With Quote