Surprisingly I couldn’t find any posts detailing this, so I’m going to do my thing.
A Common Scenario
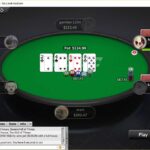
With 100bb effective stacks, EP opens for 4x preflop, there are 2 callers, and we call on the button with 9  8
8  . Both of the blinds call. The flop pot is now 24bb. The flop comes T
. Both of the blinds call. The flop pot is now 24bb. The flop comes T 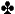 7
7  2
2  , giving us an open-ended straight draw. The BB bets 16bb and it folds to us. To decide if a call is +EV, we need to understand a little about pot odds and implied odds.
, giving us an open-ended straight draw. The BB bets 16bb and it folds to us. To decide if a call is +EV, we need to understand a little about pot odds and implied odds.
Pot Odds
Our pot odds are a ratio of the current size of the pot (before we call) to the size of bet we are calling. In our above example, after the BB bets the pot is 16bb + 24bb = 40bb and we have the option to call 16bb, making our pot odds 40:16, or 2.5:1.
Our Chance to Hit
There are 47 cards in the deck that we haven’t seen yet. Of these 47 cards, 8 will complete our straight. We call these 8 cards our "outs". Since 8 cards will complete our straight, that leaves 39 cards that do not complete our straight. The ratio of cards that aren’t outs to cards that are outs are the odds against us hitting. Here those odds are 39:8, or about 4.9:1.
Putting 2 And 2 Together
Our odds of hitting are 4.9:1 against, and our pot odds are 2.5:1. Since our pot odds are lower than our odds against hitting, we are going to be losing money if we don’t get more bets from our opponent the times we hit. To illustrate this, realize that for every 1 time we hit our draw on the turn, there are going to be 4.9 times that we miss our draw. When we hit our draw, we are winning the 2.5 units (40bb) in the pot, and when we miss our draw we are losing 1 unit (16bb) that we called. For every 1 time we win 2.5 units, there are 4.9 times that we lose 1 unit. Clearly this is a losing proposition if we don’t make more money the times we hit.
The Role of Implied Odds
Implied odds are like pot odds except they consider the money we would win from our opponent the times that we hit our draw. Suppose in our example we think that we will get an additional 50bb on average from our opponent the times we hit. This means that in addition to the 40bb pot, we will get another 50bb from our opponent the times that we hit our draw on the turn. Now we are calling 16bb to win 90bb (the 40bb pot plus our opponent’s additional 50bb), making our implied odds about 5.6:1. Since we are about 4.9:1 to hit our draw on the turn, and our implied odds are higher than that, it is a profitable play.
The Key
The key to making +EV decisions based on implied odds is to have a realistic idea of how much you stand to gain from your opponent(s) when you hit your draw. You cannot assume that you will always stack them!
Another Basic Example
On the turn you have the nut flush draw. Your opponent bets 36bb into a pot of 50bb and after you call his bet you will have 45bb left behind (and you have your opponent covered). You have 9 outs and there are 46 cards left in the deck, so that leaves 37 cards that don’t help you, so your odds against hitting are 37:9 or 4.1:1. You must fold here since the best implied odds you could be getting are 36+50+45:36 which is 131:36 or about 3.6:1.
An Example That Most New People Don’t Play Correctly
On the turn you are heads up in position and have your opponent covered. You hold 4 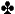 3
3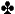 on a board of Q
on a board of Q 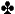 8
8 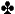 2
2  7
7  . Your opponent bets $5.60 into a pot of $8. You figure that the times you hit a flush you will get your opponent to pay off another $10 when you hit, giving you implied odds of about 4.2:1. You must fold! While this might seem like a slightly +EV call since you are about 4.1:1 against, your odds aren’t as good as they seem. First, you’re always losing against bigger flushes. Second, the 2
. Your opponent bets $5.60 into a pot of $8. You figure that the times you hit a flush you will get your opponent to pay off another $10 when you hit, giving you implied odds of about 4.2:1. You must fold! While this might seem like a slightly +EV call since you are about 4.1:1 against, your odds aren’t as good as they seem. First, you’re always losing against bigger flushes. Second, the 2 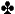 and the 7
and the 7 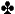 could give your opponent a full house. The lesson to be learned here is that if you’re not drawing to the nuts, you need much better implied odds.
could give your opponent a full house. The lesson to be learned here is that if you’re not drawing to the nuts, you need much better implied odds.
Now go forth and make money.
Submit your review | |